6COM2012: Social and Collective Artificial Intelligence Worksheet 3: Social Bayesian Update and Information Cascades

6COM2012: Social and Collective Artificial Intelligence Worksheet 3: Social Bayesian Update and Information Cascades

This worksheet will require you to program a solution in Python. To submit, you need to submit both the.py file and an image or a pdf of the 2 plots you generated.

1. Program a Simulation, Treasure Hunter Model

0.1 Single Agent Model

First, consider the following single-agent model. There is an agent, called a treasure hunter, who is looking for treasure. There are n = 10 locations, one of them contains infinite treasure, and the others are all empty. Each turn, the treasure hunter will take their ship, leave the harbor, and sail to one of those locations. At the beginning, they do not know where the treasure is, and assume it is equally likely for the treasure to be in any of those locations. The agent sails to the location it assumes is most likely to contain treasure. If several locations are tied for being the most likely, it will sail to one of those at random. Once it gets to the location, two things can happen. If the location is empty, then the treasure hunter agent updates its model and now assumes that there is a probability of 0.0 that this location contains treasure, and it updates its other probability assumptions accordingly. It then returns and tries again on the next turn. If the agent finds the treasure, it is very happy and takes some of the infinite treasure. There is still treasure left afterward. It then sails back home and retires. Another treasure hunter will then take their spot, and go out the next turn again searching for the treasure, starting with not knowing anything about the treasure’s location.

Implement this model in Python, and run it for 1000 turns. I recommend you write an agent class that has an internal variable, such as a vector, that stores its probability assumption for where it assumes the treasure is likely located and has several member functions. You can write an init() function to set the initial distribution of beliefs. Consider writing it in a way so you can reuse the agent class to model the new agent. Basically, the new treasure hunter that replaced the retired one, could just be the same agent, but you called init() again, to reset their values. Also write an update function that updates the internal assumptions based on finding an empty location, something like updateLocationEmpty(int). You can use a proper Bayesian Update here, but do not need it at this stage. You do not need an update function for finding the location. Also write member function int whereToGo(), which returns an integer, indicating where the agent wants to search, that is based on the agents

Now imagine there is an observer, who is looking the treasure hunters are doing. They are overlooking the harbour, and when an agent leaves, they will see where they are going. They do not observe them when they return, as it is already night at this point. So they do not know if the agent was successful or not in finding the treasure. They also cannot tell the agents apart, so they do not know if one treasure hunter retired and was replaced by another. Basically, they are just counting how many ships are going to what locations. Do you think by doing this they can gain any information about where the treasure is?

Implement some functionality that counts how many times the treasure hunters visit the various locations and output the results. This can be a graph or pure numbers at this point. Your results should look similar to those in Fig. 1.

Submitting the code and graph for the single agent model is worth 1 point.

0.2 Multi Agent Model

Now imagine a scenario with 10 treasure hunters, k = 10, each with its own independent model. They take turns going out and searching, in a fixed order. So on day 1, treasure hunter 1 goes out, on day 2 treasure hunter 2, and on day 11, it is treasure hunter 1’s turn. If someone retires, because they found the treasure, then a new treasure hunter without any knowledge just takes their spot, so there are always 10 active treasure hunters.

The treasure hunters notice that doing what they have been doing they find the treasure about 18% of the time. On their days off, they realize they can observe the other treasure hunters going out, with the same constraint as the observer from the previous example. Could they use that information to improve their own treasure hunting?

Implement a model with k = 10 treasure hunters, each with their own probability model. Then implement a member function that lets the treasure hunters use Bayesian Update based on the observed actions a of the other treasure hunters. Note that p(A|T ) can be derived from the statistics you made for observing the single agent case, where T encodes the location of the treasure. Use this to update the probability assumption of all agents. You will have to use Naive Bayesian Updating, as you will repeatedly update your distribution from observations. The prior should be the current distribution the agent has, which might already be influenced by them observing other agents previously, or actually having been to an empty location. Track how often the agents find the food, and compare it to how often agents find the food when they are not doing a Social Bayesian Update.

The treasure hunters notice that they are now basically all finding the food all the time, and their strategy works very well.

Hand in your code and a plot or image of your distributions, comparing where the agents search for treasure, with and without Bayesian Update. For this, you can set the treasure location to 1, without any lack of generality. To plot, either use some plotting library directly for python, or output the data and put them into something like Excel, both are fine. Make sure to add axis labels, and a caption to the graph.

Submitting the code and the graphs for this multi-agent part is worth 1 point, giving you the second point of two.

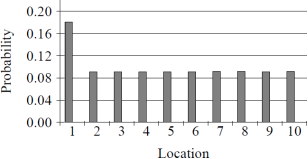
Figure 1: The probability of observing an agent going to a specific location, if the treasure is located in position 1 and there are 10 locations.

0.3 Optional: The curse of the information Cascade

This is an optional part of the worksheet, and does not net any points, but might give you a better understanding of information cascades.

While all seems fine in the world of the treasure hunters, the story unfortunately does not end here. Consider a tiny update to the model, a moving treasure hoard. Imagine, every turn there might be a tiny p(.) = 0.01 probability that the treasure moves to a new location. This does not seem like much, but what happens if you model this? To account for this move, there should be a tiny update every turn to the internal model of the agent, basically, the internal belief of the agents could be a sum of 0.99 times their current belief, plus 0.01 times an equal distribution. This introduces a tiny amount of uncertainty in the internal model. If you implement that, both the moving treasure and the updated belief function, you will see that the performance of the treasure hunters drops massively, to about 10%. You will also see that they will basically all go to one location, and even though they might have found it empty 10 turns ago when it was their last turn, they will go there again, as the Bayesian Update has overruled their internal beliefs that this is empty, and amplified that tiny uncertainty to near certainty.

Feel free to play around with this model, and find a way to improve the strategy of the treasure hunters. If you want to get some ideas or a more detailed description of the model, you can also have a look at the paper this is based.