FIT2004 Data Structures and Algorithms Assignment 01 Semester 01 2025 | MU

Programming Criteria

It is required that you implement this exercise strictly using the Python programming language(version should not be earlier than 3.5). This practical work will be marked on the time complexity, space complexity and functionality of your program, and your documentation. 

Your program will be tested using automated test scripts. It is therefore critically important that you name your files and functions as specified in this document. If you do not, it will make your submission difficult to mark, and you will be penalised. 

Submission Requirements

You will submit a single Python file containing all of the questions you have answered, assignment1.py. Moodle will not accept submissions of other file types. 

Academic Integrity

The assignments will be checked for plagiarism and collusion using an advanced detector(s).In previous semesters, many students were detected and almost all got zero marks for the assignment (or even zero marks for the unit as a penalty), and, as a result, the large majority of those students failed the unit. Helping others to solve the assignment is NOT ACCEPTED. Please do not share your solutions partially or completely with others. Even after the deadline, your solutions/approaches should not be shared before the teaching team releases the grades and feedback. Using content from the Internet, books etc without citing is plagiarism (if you use such content as part of your solution and properly cite it, it is not plagiarism; but you wouldn't be getting any marks that are possibly assigned for that part of the task, as it is not your work). 

The use of generative AI and similar tools for the completion of your assignment is not allowed in this unit! They often hallucinate bad solutions.

FIT2004 Learning Outcomes 

This assignment achieves the Learning Outcomes of: 

• Analyse general problem-solving strategies and algorithmic paradigms, and apply them to solving new problems;
• Prove the correctness of programs, analyse their space and time complexities; 
• Compare and contrast various abstract data types and use them appropriately;
• Develop and implement algorithms to solve computational problems. 

In addition, you will develop the following employability skills: 

• Text comprehension.
• Designing test cases.
• Ability to follow specifications precisely.

Assignment Timeline

In order to be successful in this assessment, the following steps are provided as asuggestion. This is an approach which will be useful to you both in future units, and in industry. 

Planning 

1. Read the assignment specification as soon as possible and write out a list of questions you have about it. 

2. Try to resolve these questions by viewing the FAQ on Ed or by thinking through the problems over time. 

3. As soon as possible, start thinking about the problems in the assignment. 

• It is strongly recommended that you do not write code until you have a solid feeling for how the problem works and how you will solve it. 

4. Writing down small examples and solving them by hand is an excellent tool for coming to a better understanding of the problem. 

• As you are doing this, you will also get a feel for the kinds of edge cases your code will have to deal with. 

5. Write down a high-level description of the algorithm you will use. 

6. Determine the complexity of your algorithm idea, ensuring it meets the requirements. 

Implementing 

1. Think of test cases that you can use to check if your algorithm works. 

• Use the edge cases you found during the previous phase to inspire your test cases.
• It is also a good idea to generate large random test cases.
• Sharing test cases is not allowed, as it does not help solve the assignment. 

2. Code up your algorithm, and test it on the tests you have thought of. 

3. Try to break your code. Think of what kinds of inputs you could be presented with that your code might not be able to handle. 

• Large inputs
• Small inputs
• Inputs with strange properties
• What if everything is the same?
• What if everything is different?
• etc... 

Before submission 

• Make sure that the input/output format of your code matches the specification.
• Make sure your filenames match the specification.
• Make sure your functions are named correctly and take the correct inputs. Remove print statements and test code from the file you are going to submit.

Documentation 

For this assignment (and all assignments in this unit), you are required to document and comment your code appropriately. Whilst part of the marks of each question are for documentation, there is a baseline level of documentation you must have for your code to receive marks. In other words:

Insufficient documentation might result in you getting 0 for the entire question for which it is insufficient. 

This documentation/commenting must consist of (but is not limited to): 

• For each function, a high-level description of that function. This should be a two or three-sentence explanation of what this function does. 
• Your main function in the assignment should contain a generalised description of the approach your solution uses to solve the assignment task.
• For each function, specify what the input to the function is, and what output the function produces or returns (if appropriate).
• For each function, the appropriate Big-O or Big-Θ time and space complexity of that function, in terms of the input size. Make sure you specify what the variables involved in your complexity refer to. Remember that the complexity of a function includes the complexity of any function calls it makes.
• Within functions, add comments where appropriate. Generally speaking, you would comment complicated lines of code (which you should try to minimise) or a large block of code which performs a clear and distinct task (often blocks like this are good candidates to be their functions!). 

A suggested function documentation layout would be as follows:

There is a documentation guide available on Moodle in the Assignment section, which contains a demonstration of how to document code to the level required in the unit.

Warning 

For all assignments in this unit, you may not use Python dictionaries or sets. This is because the complexity requirements for the assignment are all deterministic worst-case requirements, and dictionaries/sets are based on hash tables, for which it is difficult to determine the deterministic worst-case behaviour. 

Please ensure that you carefully check the complexity of each in-built Python function and data structure that you use, as many of them make the complexities of your algorithms worse. Common examples that cause students to lose marks are list slicing, inserting or deleting elements in the middle or front of a list(linear time), using the in keyword to check for membership of an iterable (linear time), or building a string using repeated concatenation of characters. Note that the use of these functions/techniques is not forbidden, however, you should exercise care when using them. 

Please be reasonable with your submissions and follow the coding practices you've been taught in prior units (for example, modularising functions, type hinting, and appropriate spacing). While not an otherwise stated requirement, extremely inefficient or convoluted code will result in mark deductions. 

These are just a few examples, so be careful. Remember that you are responsible for the complexity of every line of code you write!

Locomotion Commotion (10 marks, including 2 marks for documentation) 

In this assignment, you are expected to develop and implement an efficient algorithm to determine the least-cost path to intercept a moving passenger on a train loop. 

You have a long-awaited reunion with your friend, who has just arrived in the city. They are a passionate train enthusiast and have decided to ride the city's newly built high-speed train loop. They are so excited about the ride that they refuse to exit the train unless you are at the train station. However, due to the high volume of passengers and the ongoing development of parking infrastructure, the city imposes strict pick-up times, where you are not allowed to stop and wait at any location. Therefore, to pick up your friend, you must simultaneously arrive/intercept them at a train station. 

The city is organised into various locations connected by roads and a one-way high-speed train loop. To navigate effectively, you have obtained a city map which has two sub-maps: a detailed road map of the city and a train network map. 

The Road Map 

• There are two types of locations: regular locations and train stations. Whilst all train stations are locations, not all locations are regular locations.
• There are|L|total locations in the city, denoted byℓ0toℓ|L|−1.
• Roads connect locations, and every road has a travel cost representing the expenses of travelling along the road such as fuel or tolls.
• Every road also has an associated travel time in minutes, representing how long it takes to travel down the road.
• There are a total of|R|roads shown in the map, from r0tor |R|−1.
• All locations have at least one outgoing road to another location. 

The Train Network Map 

• The train network consists of a single circular loop with one train travelling continuously in a designated direction.
• There are|T|total train stations in the city, but due to budget constraints, the network designer could only create a maximum of 20 stations; thus, 2 ≤ |T| ≤20. 
• All|T|stations are included within the|L|locations in the road map.
• Since it is a high-speed rail, the travel time between any two consecutive stations ranges between 1 minute to 5 minutes.
• The train only makes brief stops at each station to maximise the number of passengers it can transport throughout the day, effectively having no delay at each station.

You start to manually plan out a route to precisely intercept your friend, as you know which station they will begin at and where you will begin driving from. However, as you proceed, you find that the task quickly becomes complicated and tedious. To make matters worse, you find out that you find several city maps, representing different proposed versions of the road map and the train network throughout the new city's development. You are unsure which city map is the latest and current version, and want to find an optimal route based on each one. You realise this has now turned into a complex problem that would take too long to do manually, so you turn to your algorithmic and coding prowess in hopes of getting out of this train-wreck of a situation. 

Your goal is to develop an algorithm that determines how to intercept your friend at the lowest possible cost based on a given road map and train network map. The algorithm should return the total cost incurred and the sequence of locations you must traverse, beginning at your starting point and ending at the station where you intercept your friend. 

1.1 Optimal Interception Planning 

You must create a function in Python by considering how the optimal valid route, along with the optimal pickup location, can be calculated with the provided road and train network maps. The function should return the total cost of intercepting your friend, the total time spent driving, and the list of locations you have to drive through, doing so in a way that achieves the minimum possible total cost. If it is impossible to directly intercept your friend, the function should simply return None. 

You will need to implement the function, intercept(roads, stations, start, friendStart). This function accepts four arguments:

• roads is a list of roads where each road is represented as a tuple(ℓu, ℓv, c, t)where:

ℓu∈ {ℓ0, ℓ1, . . . , ℓ|L|−1 }is the starting location of the road, 
ℓv∈ {ℓ0, ℓ1, . . . , ℓ|L|−1 }is the ending location of the road, 
c is the positive integer cost of travelling down the road fromℓutoℓv, 
It is the time in minutes as a positive integer required to travel fromℓutoℓv.

Each road is a directed road, meaning a road fromℓutoℓv does not necessarily imply there is a road fromℓvtoℓu. 

• stations is a list of train stations where each station is represented as a tuple(ℓTS, t) where:

ℓTS∈ {ℓ0, ℓ1, . . . , ℓ|L|−1 }is a train station, 

t∈ {1,2,3,4,5}is the time in minutes to travel fromℓTS to the next train station in the train loop, 

the number of stations,|T|, will be bounded such that2≤ |T| ≤20.

The tracks are provided in the order of the train loop, such that the train travels from stations[i] to stations [i + 1]. The final station, stations[|T| - 1], would loop back to stations[0].

• start∈ {ℓ0, ℓ1, . . . , ℓ|L|−1 }is the location from where you start the trip.
• friend Start∈ {ℓ0, ℓ1,..., ℓ|L|−1 }is the train station from where your friend starts their journey. It will always be referring to a valid train station instance. You can assume that friend Start will always be different from start. 

Both you and Your Friend start the Journey Simultaneously

There can be multiple valid routes that will take you from the start to a train station to meet with your friend, however, your task is to find the route that minimises the total cost. In the event there are multiple such routes, the function must return the one with the least amount of driving time as the second criterion. In the event there are multiple routes with the same optimal cost and minimum driving time, return any of the possible routes. 

Your function intercept(roads, stations, start, friend Start)should return a tuple (total Cost, total Time, route)where: 

• Total cost is the total cost of the journey along the optimal valid route. This should be a positive integer.
• Total time is the total time driven of the journey along the optimal valid route. This should be a positive integer. 
• The route is the route you can use to drive fromstartto the train station where you intercept your friend. This should be a list of integers in the range of 0 to |L| −1 that represent the locations you travel along the route, ending with the intercepting train station. 

If it is impossible to intercept your friend, your function should return None. 

1.2 Complexity 

The function must run in O (|R|log|L|)time complexity and O (|L|+|R|)auxiliary space complexity.

1.3 Examples 

In this section, we provide some examples for you to gain a better understanding of the intended behaviour and the output intercept (roads, stations, start, friendStart)function. 

Note that this list is not exhaustive, and passing the following examples does not imply your function is correct and within complexity. 

Example 1: Simple

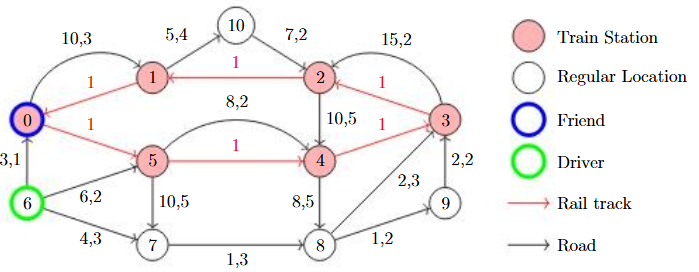
Example 1, Simple 

roads = [(6,0,3,1), (6,7,4,3), (6,5,6,2), (5,7,10,5), (4,8,8,5), (5,4,8,2), 
(8,9,1,2), (7,8,1,3), (8,3,2,3), (1,10,5,4), (0,1,10,3), (10,2,7,2), 
(3,2,15,2), (9,3,2,2), (2,4,10,5)] stations = [(0,1), (5,1), (4,1), (3,1), (2,1), (1,1)] 
start = 6 
friendStart = 0 
>>> intercept(roads, stations, start, friendStart)
 (7, 9, [6,7,8,3]) 

Your friend begins at location 0 and you begin at location 6. Notice, if you choose to move to location 7, 3 minutes would have passed and your friend would have appropriately moved 3 minutes forward, going from station 0 to station 5, then to station 4, and then finally having arrived at station 3. Alternatively, you could go to location 0, but since this takes 1 minute, your friend moves to location 5, therefore, you have missed them.Since you cannot wait at a location, you must then move to location 1.There is a possible interception route of 6→0→1→10→2with a cost of 25 but this is a larger cost than the optimal route of 6→7→8→3which has a cost of 7.

Example 2: Unsolvable 

# Example 2, Unsolvable 
roads = [(0,1,35,3), (1,2,5,2), (2,0,35,4), (0,4,10,1), (4,1,22,2), 
(1,5,65,1), (5,2,70,1), (2,3,10,1), (3,0,20,3)] 
stations = [(4,3), (5,2), (3,4)] 
start = 0 
friendStart = 4 
>>> intercept(roads, stations, start, friendStart)
 None

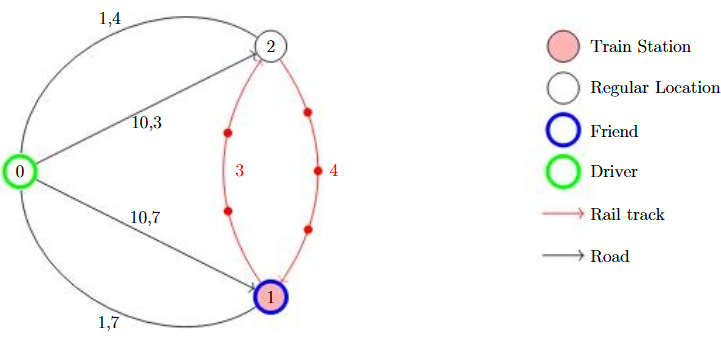
In the following example there is no way to reach your friend. Notice that each time you travel in the outer most ring, your friend also progresses to the next station. So if you travel from location 0 to location 1, your friend travels from location 4 to location 5.This pattern is highlighted in Figure 1. Anytime you attempt to intercept at a station, 1 minute passes and your friend will be ahead of you along the train track. This is shown visually where the red dots along the trail tracks represent where your friend could be along the track. This is just because when you travel to an adjacent location, your friend will not always necessarily be at a train station. The blue highlighted dot on the track just represents where your friend currently is part way along a track. Returning back to the example, after attempting to intercept and then travelling back to the outer ring "resets" the state as if you remained there. For example, travelling from location 0 to location 4, your friend is now slightly ahead. Then travelling from location 4 to location 1, your friend is now at location 5, which gives you the exact same state as if you just travelled directly to 1 from 0. This is highlighted in Figure 2.

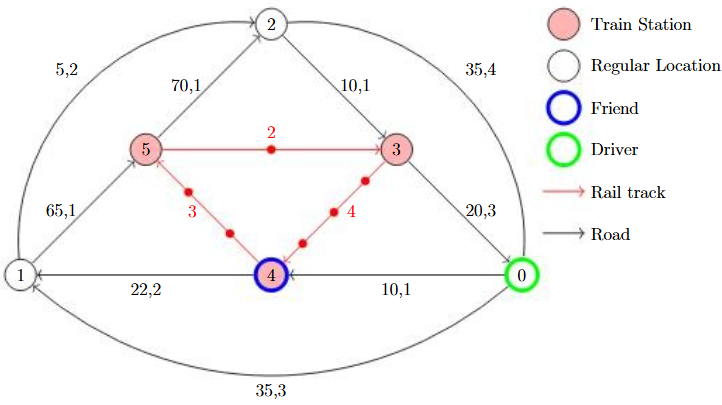
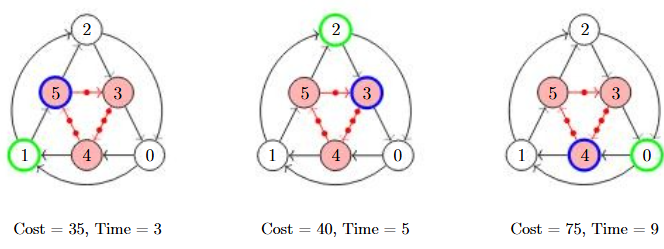
Figure 1: Simulated path following outer loop of Example 2

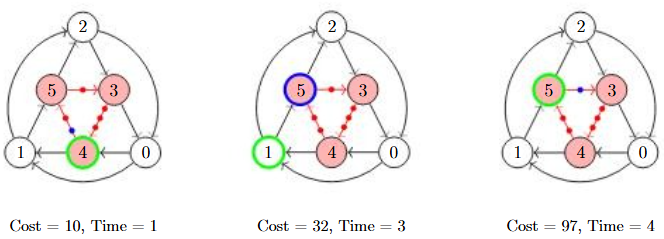
Figure 2: Simulated path attempting to intercept at station of Example 2 

Example 3: Repeated Locations 

# Example 3, Repeated Locations 

roads = [(0,1,35,7), (1,2,5,4), (2,0,35,6), (0,4,10,5), (4,1,22,3), 
(1,5,60,4), (5,3,70,2), (3,0,10,7)] 
stations = [(4,2), (5,1), (3,4)] 
start = 0 
friendStart = 3 
>>> intercept(roads, stations, start, friendStart) 
(160, 39, [0,1,2,0,1,2,0,4]) 

In this example, the optimal solution requires you to revisit a location multiple times. Notice in this example, the first time you visit a location, attempting to go to an adjacent station would result in missing your friend and therefore not intercepting them.There is a route 0→4→1→5→3with a cost of 162 but this is a larger cost than the optimal route of 0→1→2→0→1→2→0→4with a cost of 160.

Example 4: Same Cost, Different Time 

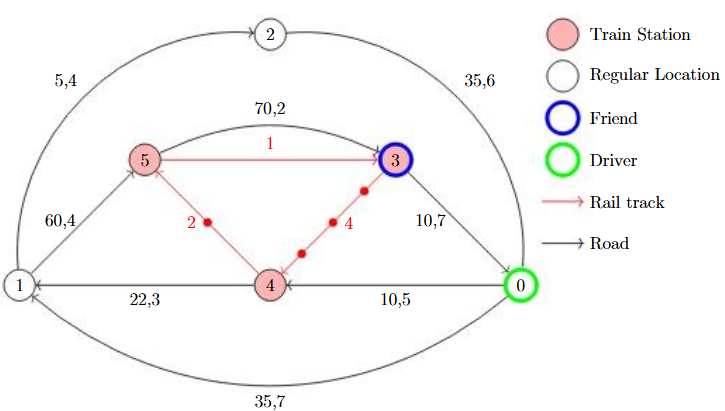
# Example 4, Multiple routes with same cost but different total time 

roads = [(0,1,10,7), (0,2,10,3), (2,0,1,4), (1,0,1,7)] 
stations = [(2,4), (1,3)] 
start = 0 
friendStart = 1 
>>> intercept(roads, stations, start, friendStart) 
(10, 3, [0,2])

In this example, there are two possible interceptions with the same cost,0→1and0→2. The latter will produce a path has a lower overall driving time.