| Category | Assignment | Subject | Mathematics |
|---|---|---|---|
| University | Dublin City University | Module Title | STAT30010 Time Series |
| Assessment Title | Assignment 1 |
|---|
Consider the time series {Xt}t∈Z Xt = β0 + β1t + β2t 2 + Wt, where {Wt}t∈Z ∼ WN(0, σ2), and β0, β1, β2 are real constants with β1 ̸= 0 and β2 ̸= 0.
(a) Show that both Xt and ∇Xt are non-stationary.
(b) Show that ∇2Xt is stationary.

Assume that {Xt} satisfies the equation (1-ϕB)Xt = Wt,
(a) Generate n = 300 observations from the process (1) with ϕ = 0.35. Plot the simulated time series and its ACF. Provide your R code. Does this generated time series look stationary?
Justify your answer
(b) Now repeat (a) with ϕ = 0.999. Plot the simulated time series and its ACF. Does this generated time series look stationary? Justify your answer
Let {Xt}t∈Z be a time series satisfying the representation Xt = − X∞ j=1 ϕ −jWt+j , t ∈ Z, (2) for |ϕ| > 1, where {Wt}t∈Z ∼ WN(0, σ2 ).
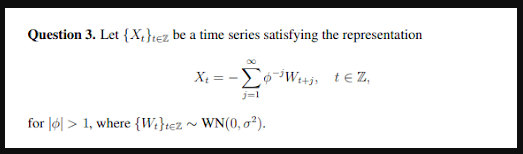
(a) Write Equation (2) in terms of backshift operators and compute the mean and variance functions of Xt. Hint: B−jYt = Yt−(−j) = Yt+j
(b) Compute the autocovariance of {Xt}t∈Z and argue that this process is stationary.
Let {Yt}t∈Z be a stationary process with mean function µ and autocovariance function cov(Yt+h, Yt) = γY (h), for h ∈ Z. Define
Xt = ∇dYt = Yt − Yt−d, t ∈ Z,
where d ∈ N. Compute the mean function and the autocovariance function of {Xt}t∈Z in terms of γY (·). Is {Xt}t∈Z stationary? Justify your answer.
Let {Wt}t∈Z ∼ WN(0, σ2). Identify the AR and MA polynomials and determine whether the following ARMA processes are causal and/or invertible. Also, watch out for parameter redundancy.
(a) Xt = −0.2Xt−1 + 0.48Xt−2 + Wt
(b) Xt = −1.9Xt−1 − 0.88Xt−2 + Wt + 0.2Wt−1 + 0.7Wt−2.
Get the Solution of this STAT30010 Assessment
Order Non-Plagiarised AssignmentLooking for expert guidance in STAT30010 Time Series? Worry no need! We are here to help you with assignments. Whether you need mathematics assignment help or well-structured solutions, we will provide everything. You will get free assignment examples that will make your study material stronger. our expert team are providing all assignment services, you will get accurate, clear, and original content. Now stop worrying about marks and complete your assignments hassle-free with expert support. So what's the delay? Get connected with us now and make your academic journey easy!
Hire Assignment Helper Today!
Let's Book Your Work with Our Expert and Get High-Quality Content
