| Category | Assignment | Subject | Mathematicsa |
|---|---|---|---|
| University | University of South Africa | Module Title | STA2603 Distribution Theory II |
Answer all questions, giving full calculations and writing any explanations in full sentences. You should submit one PDF document, which can be scanned, handwritten answers or typed and converted to PDF.
In each of the following scenarios, the respective parameter(s). Justify your answer!
(a) Suppose that drilling for water in a region is successful with probability 0.1 for each hole, independently of other holes. Let X be the number of holes where water was found, out of 5 drilled holes.
(b) A box contains 10 USB flash drives, and it is known that among them are five second-hand flash drives that already contain data. Two flash drives are randomly chosen from the box. X is equal to one if at least one of the flash drives chosen already contains data; otherwise, X equals zero.
(c) Assume that 15% of USB flash drives bought from a street corner vendor are known to be defective. One flash drive is bought from the vendor each day. LetXis the number of the day when the second defective flash drive is bought.
(d) Assume that each day of a week has the probability 0.2 of being cloudy, independently of the weather on any other day. Let X be one if both Monday and Tuesday next week are cloudy, otherwise zero.
In each of the scenarios (a)to(d) of Question1,calculate the probability thatXD1:
(a) Assume that X has a uniform distribution between -3 and +3. Find the probability that X< - 2 or X > 2 (7)
Do You Need STA2603 Assignment for This Question
Order Non-Plagiarised Assignment(b) Assume that the percentage of medium-sized businesses in Gauteng that are adequately insured has the Type I beta distribution with m 3 and n = 3. Calculate the probability that more than 75% of medium-sized businesses are adequately insured. (8)
(c) Let X be the time in days until the next breakdown of a computer server. It is known that the distribution of X is exponential with an expected value of 30 days.
Study your doc or PDF
(i) Find the median and the 90th percentile of the random variable X (11)
Upload your materials to get
(ii) Explain what the median and 90th percentile tell us about the time until the next break- (4)
Suppose that the random variable X has the following density function: [12]
![]()
Why is this page out of focus?
(a) Find the value of c (5)
(b) Because this is a premium document. Subscribe to unlock this document and more. (7)
Let us assume that a function F(x), with -1 ≤x≤ 2, is defined as follows.
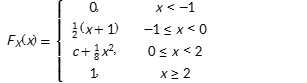
(a) Find the value of the constant c such that F is the probability distribution function of a continuous random variable X. (8)
(b) Find the density function of the random variable X. (5)
Are you trying to find someone who can help with my STA2603 Distribution Theory II? Well! You're in the right place, our podium, Workingment provides Mathematics Assignment Help. Our well-researched and talented professors can also provide you with odd assignments. Suppose you're judging whether to Write My Assignment with our professors. No doubt! Our team can help with your assignment. We also provide Free Sample assignments for your guidance. Get in touch right now!
Hire Assignment Helper Today!
Let's Book Your Work with Our Expert and Get High-Quality Content
