ISYE 3103 Supply Chain Modeling: Logistics Homework 3 Brief 2025

Instructions

You may discuss this assignment with others, but you must write your solutions independently. Please list the names of those you worked with at the top. Show all of your work, and be sure to write legibly. Submit your solution to the 'Homework 3' assignment on Canvas. 

Problem 1 [25 points] 

A biotechnology company produces boxes of pipette tips at plants in Madison and Dallas. The Madison plant can produce up to 12,000 boxes per month, and the Dallas plant can produce up to 8,000 boxes per month. Each month, pipette tip boxes must be shipped to three research institutions: 6,000 boxes to Atlanta, 7,500 boxes to Boston, and 5,500 boxes to Los Angeles. Shipments may also be routed through Phoenix and Charlotte. At most 4,000 boxes can be sent directly from any one city to any other city. The cost of shipping each box between cities is given in the table below. Cells containing '-' indicate the absence of a connection. For example, there is no arc from Madison to Los Angeles.

The goal is to find the production and distribution plan that minimises total cost and feasibly delivers pipette tip boxes from the production locations to the customer locations. 

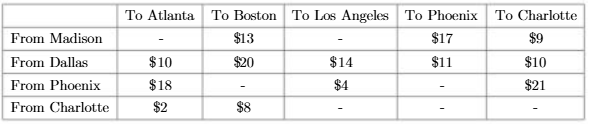
(a) (10 points) Model this problem as a minimum cost network flow. Draw the network and label all nodes. Specify the upper bounds and costs of all arcs as well as the net supplies of all nodes. You do not need to write a linear programming formulation. 

(b) (5 points) Now, suppose that at most 5,000 boxes may be shipped through Charlotte. How would you modify your network in part (a) to include this new restriction?

(c) (10 points) Let's revisit the situation in part (a) and disregard part (b). Suppose the company wants to add a restriction that the total number of boxes shipped from Madison to Phoenix and from Madison to Charlotte cannot exceed 7,000. How would you modify your network in part (a) to incorporate this new restriction? 

Problem 2 [20 points] 

You are volunteering to help organise Georgia Tech High School Math Day. As an ISyE student, one of your tasks is to design the seating chart for lunch using optimisation. Students from different schools are participating in the event, and there are ai students from each schooli∈ in [n]. The lunch will take place at a ballroom with tables of various sizes, where tablej∈[m] can seat hj people. To facilitate networking, you want to ensure that at most two students from the same school can sit at the same table. 

(a) (10 points) Model the problem of finding such a seating plan as a maximum flow. Since only the number of students from each school is known (not their names), it is enough to determine how many students from each school are assigned to each table. Explain the list of nodes and arcs in the network and the capacity of each arc. 

(b) (2 points) Suppose a feasible seating arrangement exists. What should be the optimal objective value of the problem in terms of a and h parameters? 

(c) (8 points) With your answer to part (a) as a guide, formulate the corresponding linear program. Explain how you would determine that no such seating plan exists based on your answer to part (b). 

Problem 3 [10 points] 

Suppose you have a minimum cost network flow problem given by a directed network (N, A), with net supplies for each node, and arc costs and capacities cij, uij. In class, we assume that flow on an arc can be any amount between 0 and the arc's capacity. Suppose that for a certain arc (u, v), you want to impose a lower boundauv∈(0, uuv; in other words, the flow amount on this arc must be at least this quantity. Explain how you can modify the parameters to produce an equivalent network flow instance in which the arc's lower bound is zero. [Hint: You can describe the capacity constraint for arc (u, v) as auv ≤xuv≤uuv. By redefining your decision variable, you can convert this constraint into 0≤x′uv≤u′ uv. What should be the definition ofx′uv? What should be the value of u ′ uv? What other parameters need to be modified?]

Problem 4 [25 Points]

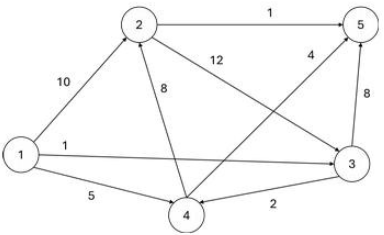
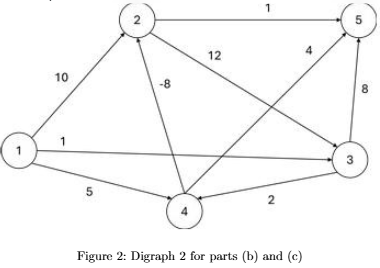
Consider the digraphs shown below with arc costs labelled (Figures 1 and 2). Use Figure 1 for part (a) and Figure 2 for parts (b) and (c). Note that the only difference between Figures 1 and 2 is the cost of (4,2): c42=8 in Figure 1 while c42=-8 in Figure 2.

Why is this page out of focus?

Because this is a premium document. Subscribe to unlock this document and more.

(a) (10 Points) Run Dijkstra's algorithm to find the shortest path from each node to node 5. Show all of your work, and be sure to clearly show the progress of the algorithm at each intermediate iteration.

(b) (10 points) Run the Bellman-Ford algorithm to find the shortest path from node 1 to node 5. Show all of your work, and be sure to clearly show the progress of the algorithm at each intermediate iteration. 

(c) (5 points) Use the Bellman-Ford algorithm to answer the following question: Does the digraph in Figure 2 have any negative-cost cycles? Justify your answer. 

Problem 5 [20 points]

A construction company is planning to build a house and needs to schedule various tasks or jobs. All jobs must be completed to complete the project. Moreover, certain jobs cannot begin until other jobs are finished; for example, drywall installation cannot begin until electrical wiring and plumbing are both complete. These precedence relations are modelled by a set of arcs A, where (i, j)∈Ameans taskimust be completed before task j can begin. You also know that each task j∈Jhas a processing time pj. Your goal is to determine a project schedule (i.e. a completion time for each jobj∈J) that satisfies all the precedence relations and completes the entire project in the shortest amount of time. Note that the company can work on multiple jobs at the same time as long as precedence relations are not violated. For example, in the instance from part (b), jobs 'a and 'b' can be worked on simultaneously.

(a) (10 points) Model this problem as a shortest path problem. Clearly explain each component of your network and/or the assumption you made to model this problem. You do not need to write an integer/linear programming formulation.

(b) (10 points) Consider the following instance:

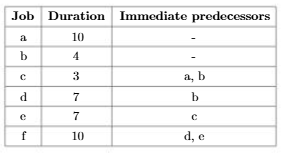
Using your approach proposed in (a), draw the network and find the shortest possible project duration. You do not need to show the step-by-step progress of your chosen algorithm