| Category | Homework | Subject | Computer Science |
|---|---|---|---|
| University | Module Title | CSC 204 - Algorithm Design and Analysis Homework 5 - Graphs |
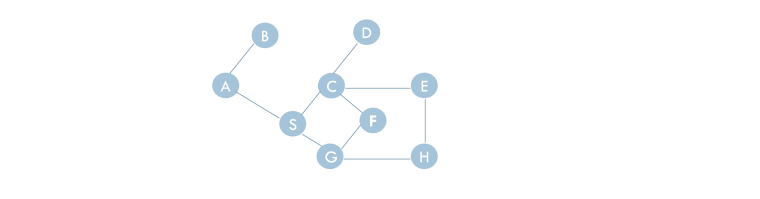
a) Given the graph above suppose we run breadth-rst-search with the source vertex as A. Assume that vertices are entered into the queue in alphabetical order. Write down the order in which the vertices would be discovered. (7 points)
b) Given the graph above suppose we run depth-rst-search. Assume that the rst vertex explored is vertex A, and that neighbor vertices are visited in alphabetical order. Write down the order in which the vertices would be discovered. (7 points)
c) State both the discovery and nishing times of each vertex after running depth-rst-search in part (b). (6 points)
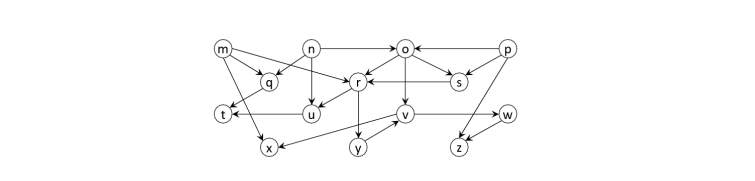
a) Show the topological sort that would be achieved after running depth rst search such that vertex m is the rst vertex explored, and the neighbor vertices are visited in alphabetical order. (5 points)
b) Draw boundaries around all of the strongly connected components of the graph below. (5 points)
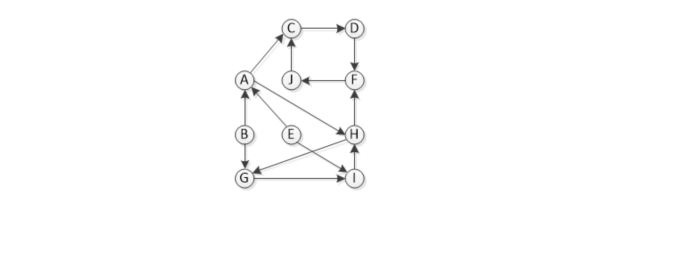
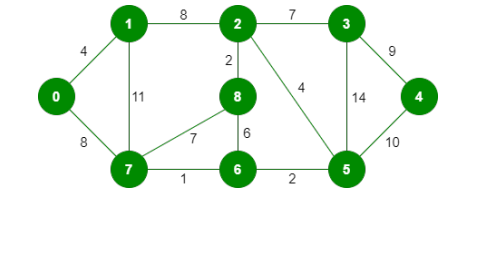
c) Perform Kruskal’s Algorithm on the graph below and draw the resulting minimum spanning tree. If two edges have the same weight, visit the edge that has the vertex ID with smallest value rst. (5 points)
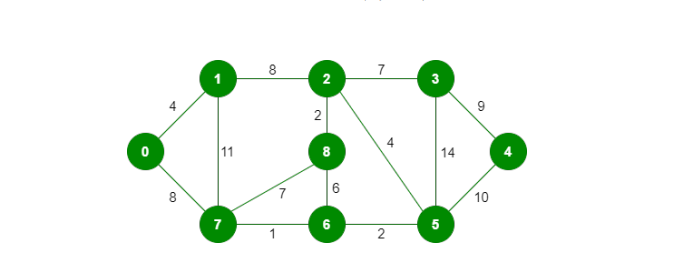
d) Perform Dijkstra's Algorithm on the graph below and state the cost of the shortest path to each vertex with vertex 0 as the source. (5 points)
a) Dijkstra's algorithm can handle graphs with negative edge weights.
b) A directed acyclic graph (DAG) always has a topological ordering.
c) A graph where all edges have distinct weights can have more than one minimum spanning tree.
d) Let T be a minimum spanning tree of a graph G. Then for any two vertices u,v the path from u to v in T is a shortest path from u to v in G.
e) A graph can have multiple topological orderings.
Hire Assignment Helper Today!
Let's Book Your Work with Our Expert and Get High-Quality Content
